| |
|
Abstract: |
Let 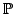 denote the collection of positive sequences defined on denote the collection of positive sequences defined on 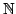 . Fix . Fix 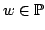 . Let . Let 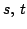 , respectively, be the sequences of partial sums of the infinite series , respectively, be the sequences of partial sums of the infinite series 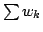 and and 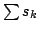 , respectively. Given , respectively. Given 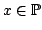 , define the sequences , define the sequences 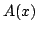 and and 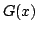 of weighted arithmetic and geometric means of of weighted arithmetic and geometric means of 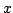 by by Under the assumption that 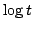 is concave, it is proved that is concave, it is proved that  for all for all 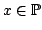 , with equality if and only if , with equality if and only if 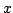 is a constant sequence. is a constant sequence.
|



