| |
|
|
| |
Volume 8, Issue 3, Article 72 |
|
|
|
|
|
| |
On the Maximum Modulus of Polynomials. II
|
| |
|
Authors: |
M. A. Qazi, |
|
| |
|
Keywords:
|
Polynomials, Inequality, Zeros. |
|
| |
|
Date Received:
|
15/02/07 |
|
| |
|
Date Accepted:
|
23/08/07 |
|
| |
|
Subject Codes: |
30D15, 41A10, 41A17.
|
|
| |
|
Editors: |
Narendra K. Govil, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let 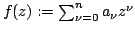 be a polynomial of degree be a polynomial of degree 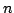 having no zeros in the open unit disc, and suppose that having no zeros in the open unit disc, and suppose that 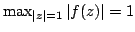 . How small can . How small can 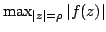 be for any be for any  ? This problem was considered and solved by Rivlin [4]. There are reasons to consider the same problem under the additional assumption that ? This problem was considered and solved by Rivlin [4]. There are reasons to consider the same problem under the additional assumption that 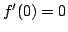 . This was initiated by Govil [2] and followed up by the present author [3]. The exact answer is known when the degree . This was initiated by Govil [2] and followed up by the present author [3]. The exact answer is known when the degree 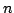 is even. Here, we make some observations about the case where is even. Here, we make some observations about the case where 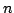 is odd. is odd.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



