A Weighted Analytic Center for Linear Matrix Inequalities

Volume 2, Issue 3, 2001

Article 29

A WEIGHTED ANALYTIC CENTER FOR LINEAR MATRIX INEQUALITIES

SCHOOL OF MATHEMATICS AND STATISTICS
CARLETON UNIVERSITY, 4370 HERZBERG
1125 COLONEL BY DRIVE
OTTAWA, ONTARIO, CANADA.
K1S 5B6
E-Mail: irwin_pressman@carleton.ca

DEPARTMENT OF MATHEMATICS AND STATISTICS
NORTHERN ARIZONA UNIVERSITY,
FLAGSTAFF AZ 86011.
E-Mail: Shafiu.Jibrin@nau.edu

Received March 21, 2001; accepted March 21, 2001.
Communicated by: J. Borwein

ABSTRACT.

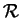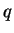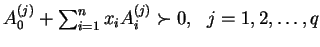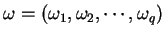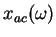Let ${\mathcal R}$ be the convex subset of ${{\rlap{\rm I}\hskip0.11em\hbox{\rm R}^{n}}}$ defined by simultaneous linear matrix inequalities (LMI) $A_{0}^{(j)}+\sum_{i=1}^{n}x_{i}A_{i}^{(j)}\succ 0, j=1,2,\dots,q$ . 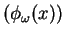Given a strictly positive vector $\boldsymbol{\omega}=(\omega_{1},\omega_{2},\cdots,\omega_{q})$ , the weighted analytic center $x_{ac}(\boldsymbol{\omega})$ is the minimizer argmin $(\phi_{\omega}(x))$ of the strictly convex function $\phi_{\omega}(x)=\sum_{j=1}^{q}\omega_{j}\log\det[A^{(j)}(x)]^{-1}$ over ${\mathcal R}$ . We give a necessary and sufficient condition for a point of ${\mathcal R}$ to be a weighted analytic center. We study the argmin function in this instance and show that it is a continuously differentiable open function.

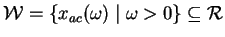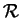In the special case of linear constraints, all interior points are weighted analytic centers. We show that the region ${\mathcal W} = \left\{x_{ac}(\boldsymbol{\omega})\mid \boldsymbol{\omega}>0 \right\} \subseteq {\mathcal R}$ of weighted analytic centers for LMI's is not convex and does not generally equal ${\mathcal R}$ . These results imply that the techniques in linear programming of following paths of analytic centers may require special consideration when extended to semidefinite programming. 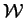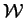We show that the region ${\mathcal W}$ and its boundary are described by real algebraic varieties, and provide slices of a non-trivial real algebraic variety to show that ${\mathcal W}$ isn't convex. Stiemke's Theorem of the alternative provides a practical test of whether a point is in ${\mathcal W}$ . Weighted analytic centers are used to improve the location of standing points for the Stand and Hit method of identifying necessary LMI constraints in semidefinite programming.

Key words:
Weighted analytic center, Semidefinite Programming, Linear Matrix Inequalities, Convexity, Real Algebraic Variety.

2000 Mathematics Subject Classification:
90C25, 49Q99, 46C05, 14P25.

Download this article (PDF):

Suitable for a printer:

Suitable for a monitor:

To view these files we recommend you save them to your file system and then view by using the Adobe Acrobat Reader.

That is, click on the icon using the 2nd mouse button and select "Save Target As..." (Microsoft Internet Explorer) or "Save Link As..." (Netscape Navigator).

See our PDF pages for more information.

Other papers in this issue

Generalized Auxiliary Problem Principle and Solvability of a Class of Nonlinear Variational Inequalities Involving Cocoercive and Co-Lipschitzian Mappings
Ram U. Verma

On Some Generalizations of Steffensen's Inequality and Related Results
P. Cerone

A Weighted Analytic Center for Linear Matrix Inequalities
I. Pressman and S. Jibrin

Good Lower and Upper Bounds on Binomial Coefficients
Pantelimon Stanica

Improvement of an Ostrowski Type Inequality for Monotonic Mappings and its Application for Some Special Means
S.S. Dragomir and M.L. Fang

On the Utility of the Telyakovskii's Class S
Laszlo Leindler

L'Hospital Type Rules for Oscillation, with Applications
Iosif Pinelis

Matrix and Operator Inequalities
Fozi M. Dannan

Consequences of a Theorem of Erdös-Prachar
Laurentiu Panaitopol

On a Reverse of Jessen's Inequality for Isotonic Linear Functionals
S.S. Dragomir

L^p-Improving Properties for Measures on R⁴ Supported on Homogeneous Surfaces in Some Non Elliptic Cases
E. Ferreyra, T. Godoy and M. Urciuolo

Some Properties of the Series of Composed Numbers
Laurentiu Panaitopol

Other issues