On Univalent Harmonic Functions

Volume 3, Issue 4, 2002

Article 61

ON UNIVALENT HARMONIC FUNCTIONS

ULUDAG ÜNIVERSITESI
FEN-ED. FAKÜLTESI
MATEMATIK BÖLÜMÜ
16059 GÖRÜKLE/BURSA
TURKEY.
E-Mail: ometin@uludag.edu.tr

Received 18 January, 2002; Accepted 26 June, 2002.
Communicated by: H.M. Srivastava

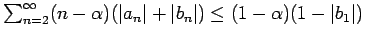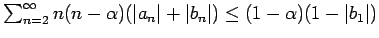ABSTRACT. Two classes of univalent harmonic functions on unit disc satisfying the conditions $\sum_{n=2}^{\infty }(n-\alpha )(\vert a_{n}\vert+\vert b_{n}\vert)\leq (1-\alpha )(1-\vert b_{1}\vert)$ and $\sum_{n=2}^{\infty }n(n-\alpha )(\vert a_{n}\vert+\vert b_{n}\vert)\leq (1-\alpha )(1-\vert b_{1}\vert)$ are given. That the ranges of the functions belonging to these two classes are starlike and convex, respectively. Sharp coefficient relations and distortion theorems are given for these functions. Furthermore results concerning the convolutions of functions satisfying above inequalities with univalent, harmonic and convex functions in the unit disk and with harmonic functions having positive real part.

Key words:
Convex harmonic functions, Starlike harmonic functions, Extremal problems.

2000 Mathematics Subject Classification:
30C45, 31A05.

Download this article (PDF):

Suitable for a printer:

Suitable for a monitor:

To view these files we recommend you save them to your file system and then view by using the Adobe Acrobat Reader.

That is, click on the icon using the 2nd mouse button and select "Save Target As..." (Microsoft Internet Explorer) or "Save Link As..." (Netscape Navigator).

See our PDF pages for more information.

Other papers in this issue

On Weighted Inequalities with Geometric Mean Operator Generated by the Hardy-type Integral Transform
Maria Nassyrova, Lars-Erik Persson and Vladimir Stepanov

Sharp Error Bounds for the Trapezoidal Rule and Simpson's Rule
D. Cruz-Uribe and C.J. Neugebauer

Rate of Convergence of the Discrete Polya Algorithm from Convex Sets. A Particular Case
M. Marano, J. Navas and J.M. Quesada

Approximating the Finite Hilbert Transform via an Ostrowski Type Inequality for Functions of Bounded Variation
S.S. Dragomir

A Polynomial Inequality Generalising an Integer Inequality
Roger B. Eggleton and William P. Galvin

On the Sequence $(p_n^2-p_{n-1}p_{n+1})_{n\ge 2}$
Laurentiu Panaitopol

On an Open Problem of F. Qi
Tibor K. Pogány

On Moduli of Expansion of the Duality Mapping of Smooth Banach Spaces
P.M. Milicic

On Generalizations of L. Yang's Inequality
Chang-jian Zhao and Lokenath Debnath

On a New Type of Meyer-Konig and Zeller Operators
Vijay Gupta