Volume 4,
Issue 1, 2003
Article
21
|
ON ENTIRE AND MEROMORPHIC FUNCTIONS THAT SHARE SMALL FUNCTIONS WITH THEIR DERIVATIVES
KIT-WING YU
RM 205, KWAI SHUN HSE.,
KWAI FONG EST.,
HONG KONG, CHINA.
E-Mail: maykw00@alumni.ust.hk
Received 28 February, 2002; Accepted 5 February, 2003.
Communicated by: H.M. Srivastava
|
ABSTRACT.
In this paper, it is shown that if 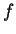 is a non-constant entire function, is a non-constant entire function, 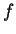 and
and 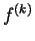 share the small function share the small function
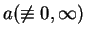 CM and CM and
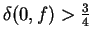 , then , then
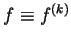 . Furthermore, if . Furthermore, if 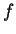 is
non-constant meromorphic, is
non-constant meromorphic, 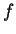 and and 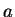 do not have any common pole and do not have any common pole and
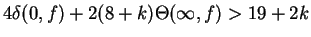 , then the same
conclusion can be obtained. Finally, some open questions are posed for the
reader. , then the same
conclusion can be obtained. Finally, some open questions are posed for the
reader.
Key words:
Derivatives, Entire functions, Meromorphic functions, Nevanlinna theory,
Sharing values, Small functions.
2000 Mathematics Subject
Classification:
Primary 30D35.
|
|
|
Download this article (PDF):
|
Suitable for a printer: 
Suitable for a monitor:
 |
To view these files we
recommend you save them to your file system and then view by using
the Adobe Acrobat Reader.
That is, click on the icon using the 2nd mouse button and
select "Save Target As..." (Microsoft Internet
Explorer) or "Save Link As..." (Netscape
Navigator).
See our PDF pages for more
information.
|
|
|
|
Other issues
-
Volume 1, Issue 1, 2000
-
Volume 1, Issue
2, 2000
-
Volume 2, Issue
1, 2001
-
Volume 2, Issue
2, 2001
-
Volume 2, Issue
3, 2001
-
Volume 3, Issue
1, 2002
-
Volume 3, Issue
2, 2002
-
Volume 3, Issue
3, 2002
-
Volume 3, Issue
4, 2002
-
Volume 3, Issue
5, 2002
-
Volume 4, Issue
1, 2003
-
Volume 4, Issue
2, 2003
-
Volume 4, Issue
3, 2003
-
Volume 4, Issue
4, 2003
-
Volume 4, Issue
5, 2003
|
|

