Generalizations of the Triangle Inequality

Volume 4, Issue 3 (GI8), 2003

Article 62

GENERALIZATIONS OF THE TRIANGLE INEQUALITY

DEPARTMENT OF MATHEMATICS,
FACULTY OF ENGINEERING,
GUNMA UNIVERSITY,
KIRYU 376-8515, JAPAN
E-Mail: ssaitoh@math.sci.gunma-u.ac.jp

Received 09 December, 2002; Accepted 15 March, 2003.
Communicated by: T. Ando

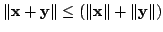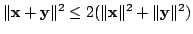ABSTRACT. The triangle inequality $\Vert \mathbf{x} + \mathbf{y} \Vert \leq ( \Vert\mathbf{x}\Vert + \Vert\mathbf{y}\Vert)$ is well-known and fundamental. Since the 8th General Inequalities meeting in Hungary (September 15-21, 2002), the author has been considering an idea that as triangle inequality, the inequality $\Vert \mathbf{x} + \mathbf{y} \Vert^2 \leq 2( \Vert\mathbf{x}% \Vert^2 + \Vert\mathbf{y}\Vert^2)$ may be more suitable. 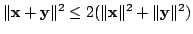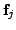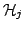The triangle inequality $\Vert \mathbf{x} + \mathbf{y} \Vert^2 \leq 2( \Vert\mathbf{x}% \Vert^2 + \Vert\mathbf{y}\Vert^2)$ will be naturally generalized for some natural sum of any two members $\mathbf{f}_j$ of any two Hilbert spaces $% \mathcal{H}_j$ . We shall introduce a natural sum Hilbert space for two arbitrary Hilbert spaces.

Key words:
Triangle inequality, Hilbert space, Sum of two Hilbert spaces, various operators among Hilbert spaces, Reproducing kernel, Linear mapping, Norm inequality.

2000 Mathematics Subject Classification:
30C40, 46E32, 44A10, 35A22.

Download this article (PDF):

Suitable for a printer:

Suitable for a monitor:

To view these files we recommend you save them to your file system and then view by using the Adobe Acrobat Reader.

That is, click on the icon using the 2nd mouse button and select "Save Target As..." (Microsoft Internet Explorer) or "Save Link As..." (Netscape Navigator).

See our PDF pages for more information.

Other papers in this issue

Report of the General Inequalities 8 Conference; September 15-21, 2002, Noszvaj, Hungary
Compiled by Zsolt Páles

Convolution Inequalities and Applications
Saburou Saitoh, Vu Kim Tuan and Masahiro Yamamoto

The Hardy-Landau-Littlewood Inequalities with Less Smoothness
Constantin P. Niculescu and Constantin Buse

Continuity Properties of Convex-type Set-Valued Maps
Kazimierz Nikodem

Carleman's Inequality - History, Proofs and Some New Generalizations
Maria Johansson, Lars-Erik Persson and Anna Wedestig

Andersson's Inequality and Best Possible Inequalities
A.M. Fink

On Some Results Involving the Cebysev Functional and its Generalisations
P. Cerone

Separation and Disconjugacy
R.C. Brown

New Norm Type Inequalities for Linear Mappings
Saburou Saitoh

An Integral Approximation in Three Variables
A. Sofo

On Some Spectral Results Relating to the Relative Values of Means
C.E.M. Pearce

On Zeros of Reciprocal Polynomials of Odd Degree
Piroska Lakatos and László Losonczi

Some New Hardy Type Inequalities and their Limiting Inequalities
Anna Wedestig

Generalizations of the Triangle Inequality
Saburou Saitoh

A Survey on Cauchy-Bunyakovsky-Schwarz Type Discrete Inequalities
S.S. Dragomir

Other issues